La ley de la elección restringida

Veamos una mano jugada en el campeonato del mundo por equipos, la final de 1973 entre Italia y USA.

	♠ A843 ♥ 1087 ♦ AQ96 ♣ K8
♠ 1097 ♥ AJ53 ♦ K873 ♣ Q7		♠ KJ6 ♥ Q94 ♦ 542 ♣ 10932
	♠ Q52 ♥ K62 ♦ J10 ♣ AJ654

 

Sur	Oeste	Norte	Este
Paso	Paso	1♦	Paso
2♣	Paso	Paso	Paso

 

En ambas salas NORTE abrió en tercera posición de 1♦ y SUR pasó los 2♣ del pártner. Ambos OESTE salieron de ♠ para el K♠ de ESTE y ambos ESTE, Garozzo y Goldman, contratacaron de la Q♥. Pues bien, los declarantes sabían que si el contrataque viene de QJ9 es preciso no poner el K para no perder 3 bazas seguidas. Pero también sabían que si el contrataque venía de Qxx debían poner el K. Los dos declarantes, Bianchi y Wolf, leyeron la posición y pusieron el K y cuando OESTE ganó con el As y salió de pequeño los dos pusieron el 10 del muerto. ¿Cuál es la explicación del acierto de los dos declarantes? El nivel era alto pero ellos aplicaron la llamada ley "Restricted Choice". Si OESTE tiene QJx puede optar por salir del  J o de la Q, en cambio con Q9x no tiene elección, debe salir de la Q.

 

Con

	AK10xx
		N
	O		E
		S
	xxxx

 

cuando juegas el As, ESTE da la Q. La mayoría de jugadores entran en SUR y juegan hacia el 10. Ponen el 10 aplicando el principio de no elección. Con QJ tenían la posibilidad de dar la Q o el J, piensan que si dan la Q es porque no tenían elección.

 

Cuidado con

	KJ3
		N
	O		E
		S
	A964

 

Aquí jugamos el 4 para el J que gana la baza y cuando jugamos el K, OESTE da la Q. Aquí no hay aplicación de la ley, cualquier jugador mediano dará la Q con Q10x, la carta conocida. Siempre es bueno dar la carta que se sabe que tenemos. Si damos el 10 el declarante no tiene dudas, sabe la posición de la Q. Solo un neófito inocente jugaría el 10. Por tanto no hay ley.

 

En un principio podríamos pensar que la ley de la elección restringida no tiene fundamento: "Que un jugador muestre una carta no significa que ahora tenga menos probabilidades de tener una carta equivalente, seguirá teniendo las mismas probabilidades que antes". Sin embargo, la ley es  un ejemplo de inferencia bayesiana y su aplicación es parecida al conocido problema de Monty Hall.

 

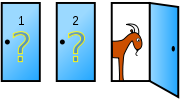
Si escogemos la puerta 1 y el presentador nos abre la puerta 3 demostrando que en ella no está el coche debemos aceptar su oferta de cambiar de puerta y quedarnos con la 2.